【新威设备如何实现GITT测试?】 -新威软件篇

【7.6.0软件打开数据不全或下载失败解决办法】-新威FAQ常见问题
2018-01-15
【如何使用新威软件设定SOC充放电?】-新威软件篇
2018-02-01GITT(Galvanostatic Intermittent Titration Technique)恒电流间歇滴定技术
恒电流问歇滴定技术(galvanostatic intermittent titration technique)由德国科学家W.Weppner提出, 基本原理是在某一特定环境下对测量体系施加一恒 定电流并持续一段时问后切断该电流,观察施加电流段体系电位随时间的变化以及弛豫后达到平衡的电压,通过分析电位随时闾的变化可以得出电极过 程过电位的弛豫信息,进而推测和计算反应动力学信息。
当体系满足如下条件时,可以计算锂离子扩散系数
1、电极体系为等温绝热体系;
2、电极体系在施加电流时无体积变化与相变;
3、电极响应完全由离子在电极内部的扩散控制;
4、τ≤L2/D,L为离子扩散长度;
5、电极材料的电子 电导远大于离子电导等条件
GITT测试由一系列“脉冲+恒电流+弛豫”组成。
弛豫过程就是指在这段时间内没有电流通过电池。因此,GITT主要设置的参数有两个:电流强度(i)与弛豫时间(t)
GITT首先施加正电流脉冲,电池电势快速升高,与iR降成正比(图中橙色箭头标注)。其中,R是整个体系的内阻,包括未补偿电阻Run和电荷转移电阻Rct等。
随后,维持充电电流恒定,使电势缓慢上升。这也是GITT名字中“恒电流”的来源。此时,电势E与时间t的关系需要使用菲克第二定律进行描述。菲克第一定律只适应于稳态扩散,即各处的扩散组元的浓度只随距离变化,而不随时间变化。实际上,大多数扩散过程都是在非稳态条件下进行的。对于非稳态扩散,就要应用菲克第二定律了。
接着,中断充电电流,电势迅速下降,下降的值与iR降成正比。最后,进入弛豫过程。在此豫期间,通过锂离子扩散,电极中的组分趋向于均匀,电势缓慢下降,直到再次平衡。
重复以上过程:脉冲、恒电流、弛豫、脉冲、恒电流、弛豫……,直到电池完全充电。放电过程与充电过程相反。
GITT的核心公式:
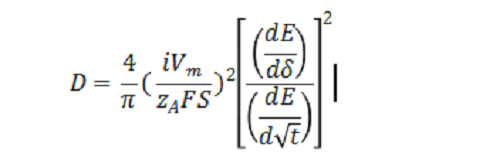
扩散系数D,是我们的目标。只要计算出公式中的每一项,D就自然得到了。
其中:
i是电流值,是我们自己设定的,【已知】;
F是法拉第常数(96485 C/mol),【已知】;
zA是离子的电荷数,锂离子是1,【已知】;
S是电极/电解质接触面积,【已知】;
dE/dδ是库仑滴定曲线的斜率,【未知】;
dE/d√t电势与时间的关系,【未知】 。
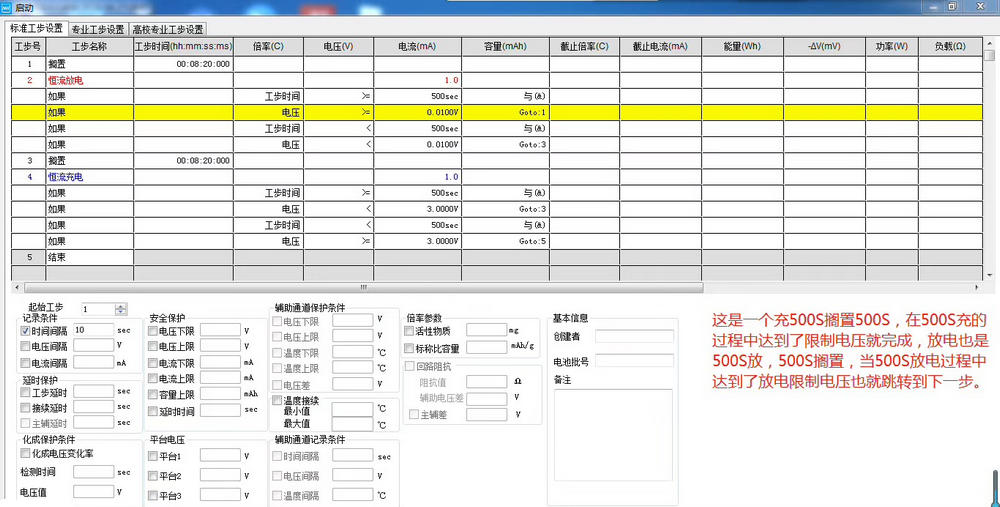
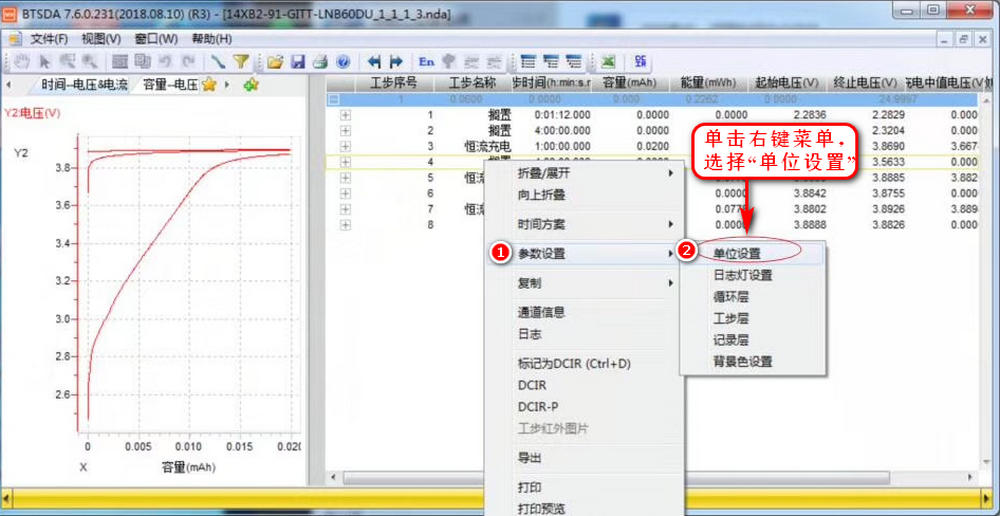
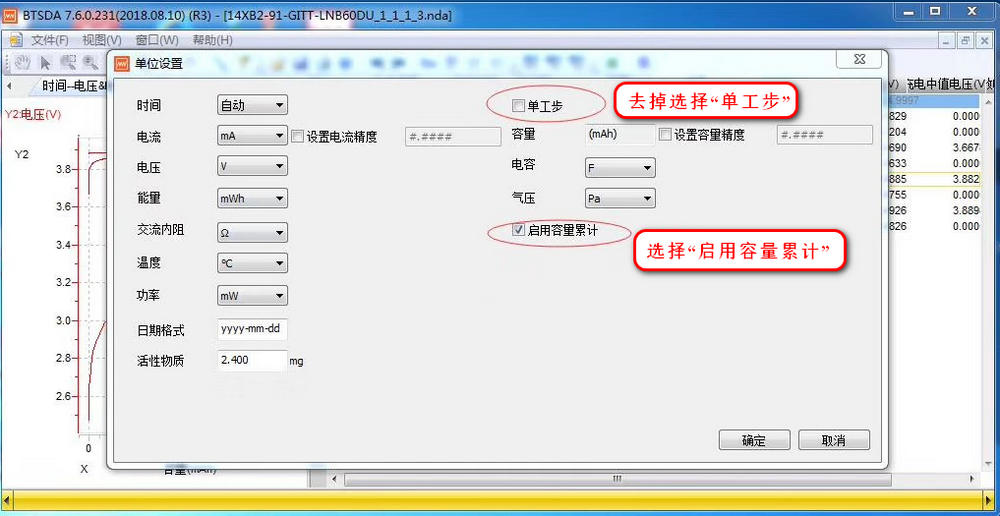
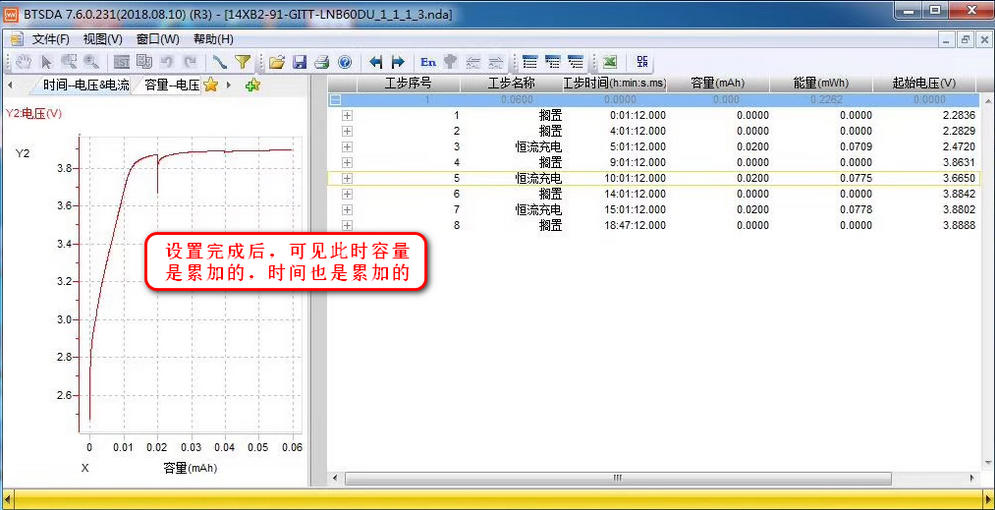
那么用新威的设备该如何进行GITT的测试设置呢?
按照如下流程即可: